TSALBP: Time and Space constrained Assembly Line Balancing Problems
Table of contents
Problem Description
In a production system made up of several branched manufacturing and/or assembly lines, the balancing of lines is a frequent problem. This is the case of the automobile industry, in which it is common to use the same line for variants of a component (e.g. chassis, body, seats, etc.), or the same painting line for the bodies of different vehicles with their variants, or the same body line for variants of the same vehicle. The need for balancing is present in different situations, even if the balancing is temporary in nature. However, some of the causes for balancing an assembly line affect the allocation of surfaces allotted to these, on both sides of the line as well as in the areas of aerial transport. If an installation already exists the limitation of the space allotted to materials and to manufacturing and assembly tools will also have to be taken into account.
This limitation of a spatial nature may be contemplated by associating with each task a required area (a function of the cycle time c, of the production mix and of the supply rate of materials) and by associating to each station an available area.
This leads us to a family of problems that we call TSALBP: Time and Space constrained Assembly Line Balancing Problems, which may be stated in the following way: given a set of n tasks with their temporal tj and spatial aj attributes (1≤j≤n) and a precedence graph, each task must be assigned to a single station such that: (1) all the precedence constraints are satisfied, (2) no station workload time is greater than the cycle time and (3) no area required by the station is greater than the available area per station.



Tipology
TSALBP presents diverse variants depending on the elements m, the number of workstations, c, the cycle time, and A, the available area per workstation. And thus, eight variants for TSALBP (see Table 1), depending on the elements, appear.
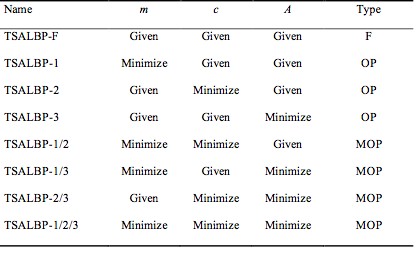
Table 1. TSALBP typology. The suffixes 1,2 and 3 refer to the minimization of m, c and A, respectively. If the problem is one of feasibility, this is indicated by F in the column “Type”; if it is a mono-objective optimization problem, this is indicated by OP; if it is a multi-objective optimization problem, this is indicated by MOP. When the problem is MOP, the suffixes 1, 2 and 3 are concatenated with “/” to name the problem.
For example, TSALBP-1 (equivalent to SALBP-1, if A → ∞) consists in minimizing the number of stations m given fixed values of the cycle time c and of the available area per station A, whereas TSALBP-F is a feasibility problem given fixed values of m, c and A.